2024 iThome 鐵人賽

DAY 27

Security

「後量子密碼學」- 未來資訊安全的基礎系列第 27 篇

Day27 RS 編碼的錯誤更正機制！

16th鐵人賽

cesare381

2024-10-08 23:16:46

63 瀏覽

分享至

昨天我們討論了 RS 編碼，今天來討論他的錯誤更正機制。
回憶一下 Hamming Code ，他可以更正一個錯誤，並且有個快速漂亮的演算法來修正該錯誤。所以今天我們也要討論兩個問題：

RS 編碼可以更正幾個錯誤？
RS 編碼如何更正錯誤？

簡要複習 RS 編碼

訊息為

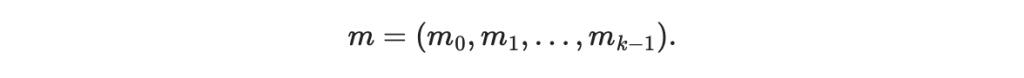
會先做出「訊息多項式」

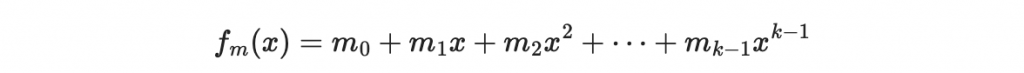
再代點進去形成編碼

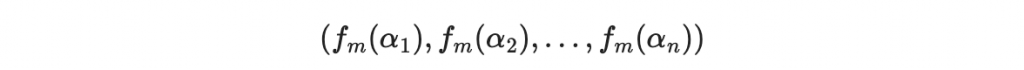
如果傳遞過程沒有錯誤，接收者可以直接用插值法計算回「訊息多項式」，把係數讀出來即可得到訊息。

更正機制

現在假設傳遞過程中出現 e 個錯誤，我們等等會討論 e 必須在哪個範圍以內才能做更正。

意思是說，接收者收到的是

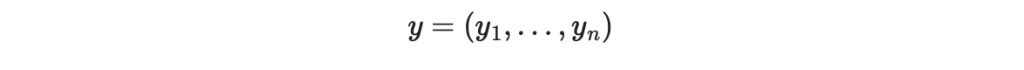
其中有 e 個 y_i 是錯的，其他都滿足

錯誤位置多項式 Error Locator Polynomial

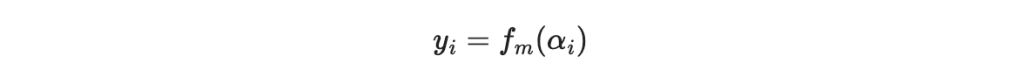
我們考慮一個多項式 E(x)

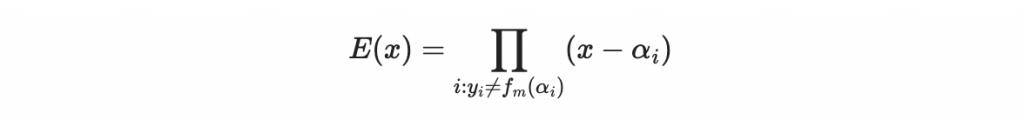
舉例，如果在 i = 1, 2, 4 時編碼傳遞出現錯誤，則

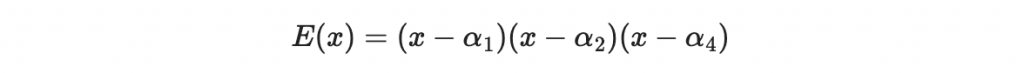
這個多項式叫做錯誤位置多項式。錯誤位置多項式的特性是，它在每個錯誤位置 alpha_i 都為 0，意思是說，通過計算 E(x)，我們能夠定位出訊息中出現錯誤的位置，這在後續的錯誤更正過程中至關重要

如果我們的編碼有 e 個錯誤，則

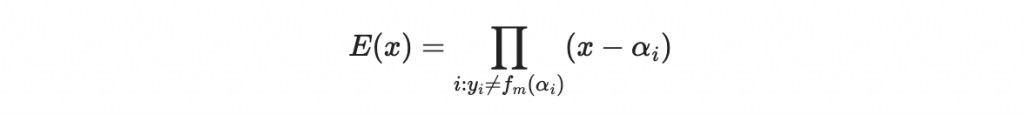
會是 e 次，且領導係數等於1。

我們將使用這個錯誤位置多項式，來推導解決 RS 編碼中錯誤位置與內容的關鍵等式。

一個關鍵的等式

因為傳遞過程有錯誤，所以在錯誤的地方

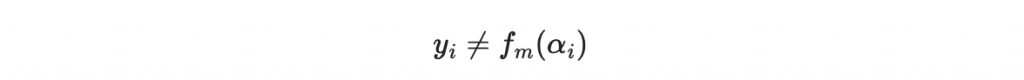
但是如果你在兩旁都乘以 E(x) ，那麼

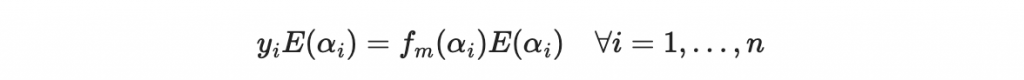
因為 E 多項式把錯誤的插值點都「零掉了」。

現在我們把右手邊寫成

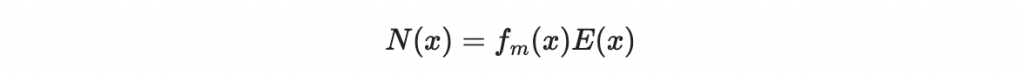
則這個關鍵等式變成

最後的一些觀察

訊息多項式

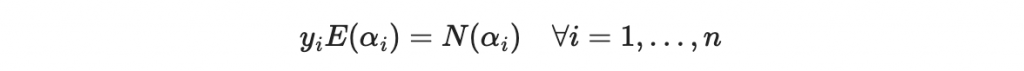
因為

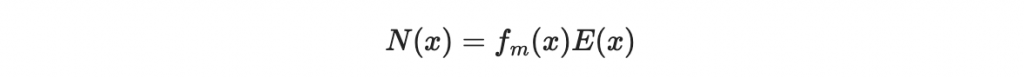
所以如果我們可以求到 N(x) 以及 E(x) ，則

對付 N(x) 與 E(x)

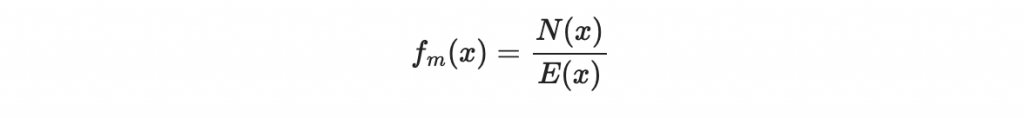
如果我們的編碼有 e 個錯誤，則

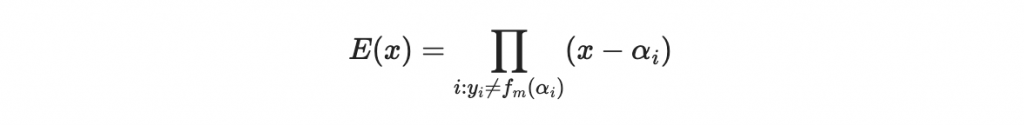
會是 e 次，且領導係數等於1。

你以為你這樣可以算 E 嗎？並沒有！因為我們不知道 y_i 在哪個 i 出錯，所以不能直接算。

我們必須假設

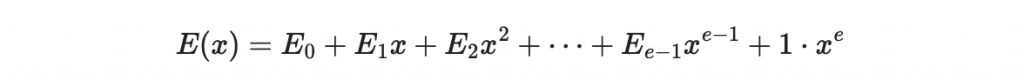
共有 e 個未知數。

另外因為

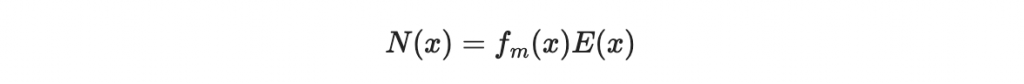
於是

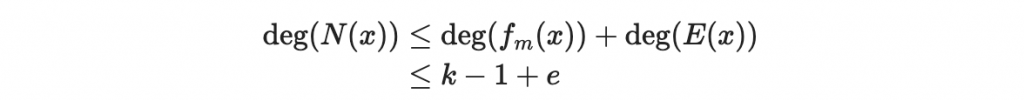
假設

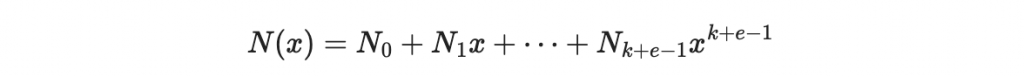
共有 k+e 個未知數。

從關鍵等式

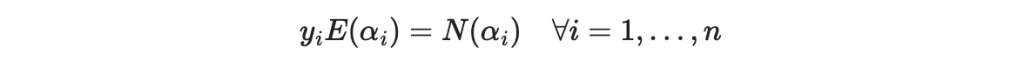
我們有 n 個條件可以用：

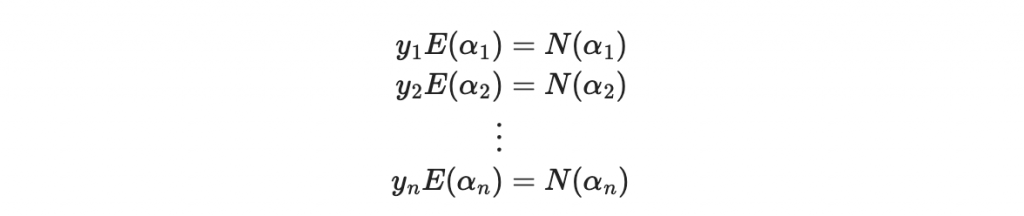
好！我們共有 e + (k+e) = k + 2e 個未知數，然後有 n 個條件，解出唯一解的條件就是：

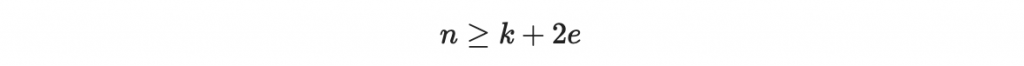
移向得到

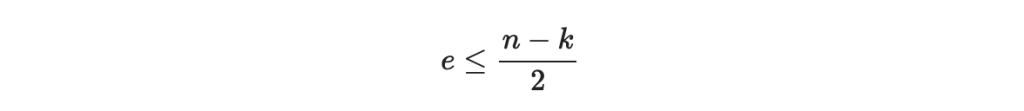
這告訴我們，當 e 小於 (n-k)/2 時，RS 編碼才能進行更正。否則 e 大於 (n-k)/2 時，我們的未知數是比條件還要多，解不回唯一的 E(x) 與 N(x) ，也就解不回訊息多項式

解關鍵等式的細節

我們來細看解關鍵等式的步驟，這是 RS 編碼錯誤更正的核心。

首先該等式為

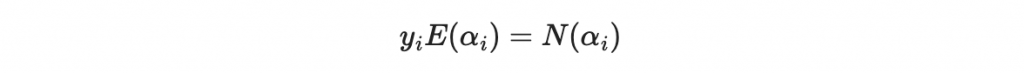
其中

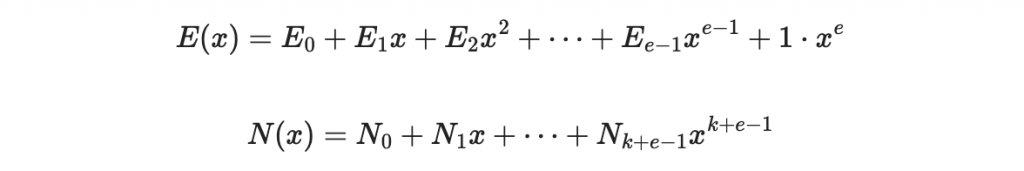
因此可以寫出：

將未知數寫在左邊，常數項寫在右邊：

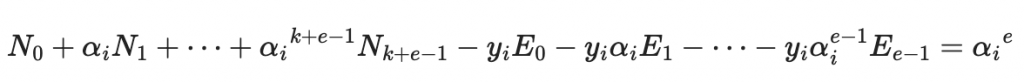
因此可以寫成矩陣方程

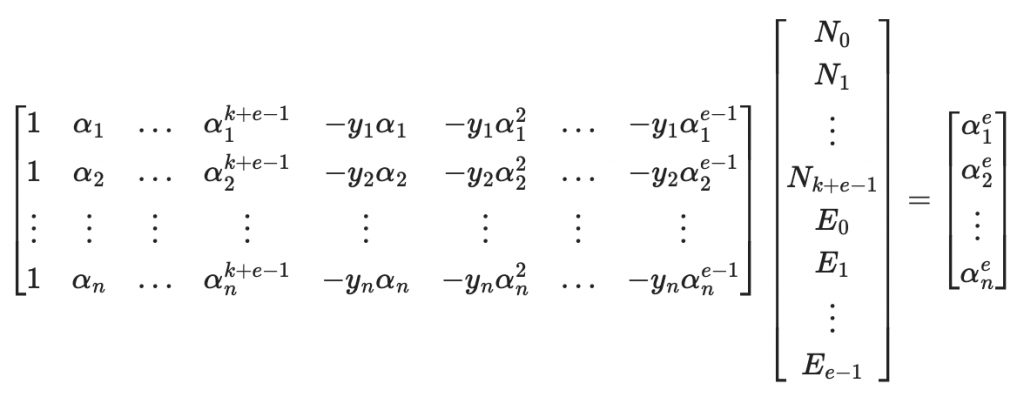
然後進行高斯消去法即可解得 N(x) 與 E(x) ，相除即可得到訊息多項式！

SageMath 實作

延續上次使用的參數以及訊息：

q = 17
n = 7
k = 3

我們使用以下的 Channel function 來模擬雜訊，其中 num_of_error 是最大錯誤數量，因為我們這裡是

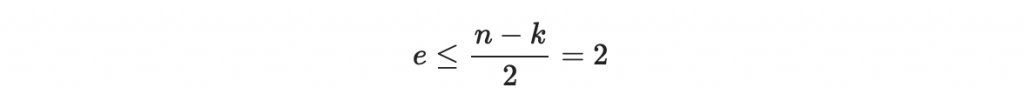
所以我們用 num_of_error = 2

def ChannelNoise(encoded, num_of_error):
    result = encoded.copy()
    actual_num_of_error = randint(0, num_of_error)
    for i in range(actual_num_of_error):
        error_position = randint(0, n-1)
        error = R.random_element()
        result[error_position] += error
    return result

received = ChannelNoise(encoded,2)
print(f"原始碼字: {encoded}")
print(f"接收到的: {received}")

# Outputs:
# 原始碼字: [10, 4, 8, 6, 16, 12, 10]
# 接收到的: [10, 4, 8, 6, 16, 2, 14]

解關鍵等式

# 解關鍵等式
# 我們需要找到一個 e 次多項式 E(X)，這個多項式用來定位錯誤位置，並找到一個 e+k-1 次的多項式 N(x)，
# 它包含了訊息與錯誤更正的組合。
# 接收的資料應滿足以下條件：received[i] E(alpha[i]) = N(alpha[i])，這樣我們可以利用這些條件來解出 E(x) 和 N(x)。


e = (n - k + 1)//2 #e = 2

LinearSystem = []
for i in range(n):
    LinearSystem.append(
        [alphas[i]^j for j in range(e+k)] + [-received[i] * alphas[i]^j for j in range(e)]
    )
print(matrix(LinearSystem))

constant_term = []
for i in range(n):
    constant_term.append( [received[i] * alphas[i]^e])

print()
print(matrix(constant_term))

print()
solution = matrix(LinearSystem).solve_right(matrix(constant_term))
print(solution.list())


# Outputs:

# [ 1 13 16  4  1 15  8]
# [ 1 16  1 16  1 13  4]
# [ 1  7 15  3  4  9 12]
# [ 1 14  9  7 13 11  1]
# [ 1  2  4  8 16  1  2]
# [ 1  9 13 15 16  5 11]
# [ 1  1  1  1  1  7  7]

# [15]
# [ 4]
# [ 1]
# [ 3]
# [13]
# [ 3]
# [10]

# [6, 3, 7, 3, 1, 1, 0]

關鍵等式的結果：

N = solution.list()[:e+k]
E = solution.list()[e+k:]

print(N,E)

# Outputs:
# [6, 3, 7, 3, 1] [1, 0]

計算回訊息多項式：

R_poly = PolynomialRing(R, 'X')
print(R_poly(N)/R_poly(E+[1]))
print(R_poly(message))

print(R_poly(N)/R_poly(E+[1]) == R_poly(message))

# Outputs:
# X^2 + 3*X + 6
# X^2 + 3*X + 6
# True